
Revista Multidisciplinar Epistemología de las Ciencias
Volumen 1, Número 1, 2024
DE LA DIVISIBILIDAD A LAS TERNAS PITAGÓRICAS: TEOREMAS Y
FORMAS DE GENERACIÓN
FROM DIVISIBILITY TO PYTHAGOREAN TRIALS: THEOREMS AND
FORMS OF GENERATION
Alexander José Villarroel Salazar
Francisco Javier Villarroel Rosillo
Venezuela

33 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
De la divisibilidad a las ternas pitagóricas: teoremas y formas de generación
From divisibility to pythagorean trials: theorems and forms of generation
Alexander José Villarroel Salazar
alexvills76@gmail.com
https://orcid.org/0000-0002-4628-1894
Investigador independiente
Venezuela.
Francisco Javier Villarroel Rosillo
fjvillr02@gmail.com
https://orcid.org/0000-0002-9159-5892
Investigador independiente
Venezuela.
RESUMEN
Este artículo se plantea un enfoque innovador, desde la perspectiva de la divisibilidad hacia la
generación de las ternas pitagóricas tomando los naturales desde n=3 y hasta infinito y sus
características de divisibilidad en base a su paridad para usar a, sus divisores y cocientes en la
generación de teoremas que permiten estudiar las posibles ternas pitagóricas que surgen de
cada número n al considerarlo como un cateto menor fijo, además se introduce una fórmula
general que permite estudiar cual es la diferencia que se desea tener entre el cateto mayor
para hallar formas iterativas y fácilmente programables para obtener la generación de ternas
pitagóricas.
Palabras claves: teorema de pitágoras, ternas pitagóricas, divisibilidad, números naturales.
ABSTRACT
This article proposes an innovative approach, from the perspective of divisibility towards the
generation of Pythagorean triples, taking the naturals from n=3 and up to infinity and their
divisibility characteristics based on their parity to use a, its divisors and quotients in the
generation of theorems that allow studying the possible Pythagorean triples that arise from each
number n when considering it as a fixed minor leg, in addition a general formula is introduced

34 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
that allows studying what difference is desired between the major leg to find iterative and easily
programmable ways to obtain the generation of Pythagorean triples.
Keywords: pythagorean theorem, pythagorean triples, divisibility, natural numbers.
Recibido: 12 de diciembre 2024 | Modificación: 16 de diciembre 2024
| Aceptado: 29 de diciembre 2024
INTRODUCCIÓN
La generación de ternas pitagóricas aún es uno de los problemas que a pesar de tener
más de 2500 años de descubierto, no ha sido explorado en forma efectiva y muchos
matemáticos solo se limitan a compartir métodos inicialistas y archiconocidos como el de la
tabla Plimpton, el uso de fracciones como lo hizo primeramente Pitágoras, el uso de estrategias
como la de la tablilla Plimpton 322 (según Robson (2002, pag 105-119) y Mansfield(2017)), las
de Diofanto, el método binomial de newton, por el cuadrado de una suma, por los números de
Fibonacci y formas de trabajo de otros matemáticos, pero es poco lo que se ha avanzado en
métodos novedosos que permitan poder generar ternas pitagóricas de una manera efectiva y
sin el conjunto de limitaciones iniciales como las dudas de si es una terna que verdaderamente
cumpla con el teorema de Pitágoras.
Martín (2023, p.1) afirmó que “el teorema de Pitágoras se encuentra en una tablilla
babilónica 1.000 años anterior al matemático”, es decir, que aunque se atribuye a Pitágoras su
proposición, formalización y demostración es de muy antigua data.
Alegría (2018) refiere en forma interesante ¡Quién le iba a decir a Pitágoras que su teorema,
caso de que fuera realmente suyo, iba a entretener al colectivo matemático veinticinco siglos
después! Refiriéndose a la gran relevancia que tiene el teorema desde su origen hasta la
actualidad.
Es por ello que puede afirmarse que es uno de los teoremas más antiguos de la
humanidad y de gran importancia en las matemáticas; al respecto González (2008) afirma que:
"el Teorema de Pitágoras es de gran uso en el ámbito de las matemáticas y es fundamental en
35 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
muchos de los teoremas geométricos que abarcan a los polígonos y los poliedros, y de gran
uso en la Geometría Analítica y de la Trigonometría" (p. 104).
Sin embargo, a pesar del larguísimo periodo existencial del teorema de Pitágoras,
muchos matemáticos se limitan a hacer repeticiones de métodos anteriores en los cuales
basan sus artículos y otros hacen aportes incompletos a la posible generación de ternas o
tripletes pitagóricos, ya que generan solo una parte muy pequeña de ellas sin hacer
aportaciones significativas, que muestren originalidad o un abordaje novedoso de las ternas
pitagóricas que genere nuevas formas de conceptualización sobre las mismas.
En este artículo luego de un minucioso proceso de revisión documental y análisis de la
temática de las ternas se llega partiendo de los aspectos de divisibilidad en el conjunto N y la
necesidad de innovar en la creación de teoremas, fórmulas y métodos de trabajo iterativos y
fácilmente programables que permiten mejorar los procesos de cálculo de ternas pitagóricas y
tener ideas muy clarificadoras de los procesos básicos de la obtención de los valores que
satisfacen el teorema de Pitágoras en cada caso.
METODOLOGÍA
1. Preliminares
Para entender la forma en que se obtuvieron los resultados que ya se han indicado
brevemente en el resumen y la introducción de este artículo se hace fundamental tratar una
serie de aspectos que consideramos importantes en el proceso de revisión, estudio y
cuestionamiento personal acerca de las triadas pitagóricas entre los cuales están los aspectos
que se relacionan con divisibilidad, números naturales, ternas pitagóricas y teorema de
Pitágoras.
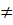
36 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
1.1. Divisibilidad
Según Jiménez (2013, p.43) y Roldán (2024, p.6) al hablar de división define la misma
diciendo por medio de la siguiente definición: “Sean a, b ∈ Z, a 0. Diremos que “a” divide a “b”,
si existe q ∈ Z tal que b = aq.”
Notación: la expresión a divide a b, se denota por a|b, y cuando a no divide a b, se denota por a
∤ b.
Sobre aspectos de división Zaldívar muestra el siguiente teorema:
Teorema 50
Sean a, b, c ∈ Z
1. Si a|b entonces (∀c ∈ Z)(a|bc).
2. Si (a|b ∧ b|c) entonces a|c.
3. Si (a|b ∧ a|c) entonces (∀m, n ∈ Z)(a|(mb + nc)).
4. Si (a|b ∧ b|a) entonces (a = b ∨ a = −b).
5. Si (a|b ∧ a > 0 ∧ b > 0) entonces a ≤ b.
Por su parte Zaldívar (2013) al hablar sobre divisibilidad expresa que:
Si a, b son dos enteros, con b ≠ 0, diremos que a divide a b, o que b es múltiplo de a, si existe
otro entero q tal que b = aq. Usaremos la notación a ∣b para decir que a divide a b y también
diremos que a es un divisor de b. Si a no divide a b lo denotaremos mediante a∤b. La relación
de divisibilidad satisface las propiedades siguientes:
Proposición I.1.
1) a ∣a, para todo a ≠ 0.
2) Si a∣b y b∣c, entonces a ∣c.
3) 1∣a, para todo a ∈ Z.
4) a∣0, para todo a ≠ 0.
37 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
5) Si a∣b, entonces a∣br, para cualquier r ∈ Z.
6) Si a∣b y a∣c, entonces a ∣b + c.
7) Si a∣b y a∣c, entonces a divide a cualquier combinación lineal de b y c, esto
es, a∣br + cs, para cualesquiera r, s ∈ Z.
8) Si a∣b, entonces a∣−b, −a∣b, −a∣−b, ∣a∣∣∣b∣.
9) Si a∣b y b∣a, entonces a = ±b.
10) Si a∣1, entonces a = ±1.
11) Si a∣b, entonces ∣a∣ ≤ ∣b∣.
Aquí la divisibilidad será utilizada en el contexto de las ternas pitagóricas estudiando
solo la divisibilidad con los divisores de igual paridad que sean menores al dividendo que es el
cateto menor de cada terna y dicha divisibilidad se estudiará considerando todos los números
naturales mayores que 3 que es el mínimo valor para el cual se forma una terna no nula o
trivial.
1.2. Números naturales
Todo número positivo desde el 1 hasta infinito pertenece a los números naturales.
Según un estudio de Graña et al. (2009, p.21) “los números naturales son, denotados con N
son los que comúnmente se usan para contar o enumerar, es decir, 1,2,3,4,5 y así
sucesivamente y que ayudan a decir cuántos elementos posee un conjunto cualquiera”.
Referente a este tema, Jiménez et al. (2004, p.1) y Pérez Porto y Merino (2009, p.1) al hablar
en relación a los números naturales dicen lo siguiente: “Los números naturales pertenecen al
conjunto de los números enteros positivos y se encuentran a la derecha del cero en la recta
real. Además, conforman un conjunto infinito, ya que incluyen a todos los elementos de una
sucesión 1, 2, 3, 4, 5, …). Dicho conjunto N es cerrado para las operaciones de suma y
multiplicación, ya que, al operar con cualquiera de sus elementos, el resultado siempre será un

38 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
número natural.” La propiedad de cierre en cuanto a la suma y la multiplicación es
aprovechada en cuanto a las modularidades de los números compuestos.
Según Ramos (2010) y m-Romero (2022) citando a Lane y Birkhoff (1999) señala que “Los
números naturales son el conjunto de números con los que se puede contar la cantidad de
elementos en un conjunto”. Este conjunto se denota con la letra , así tenemos que el conjunto
ℕ está formado por los elementos:
Aquí se usarán los números naturales para generar ternas cuyas componentes son
números naturales, es decir, que todos los elementos de una terna tendrán signo positivo y
serán enteros.
1.3. Ternas pitagóricas
Fallas (2009, pp. 1-2) y Artacho (2022, p.1) señalan que “A una terna de números naturales
que satisface la ecuación:
se llama terna pitagórica. Al correspondiente triángulo rectángulo de catetos con medidas
e hipotenusa con medida se le llama triángulo pitagórico”.
Por otra parte, Según Rodríguez (2014, p.5) y Arenzana (2019, p.1) “Una terna pitagórica es
una triada ordenada de componentes (x, y, z) que son respectivamente lados de un triángulo
rectángulo, en el cual x e y son catetos y z es la hipotenusa”. Es decir, se cumple el teorema
de Pitágoras:
Puede verse que la y la son la misma solamente que cambia
la forma de llamar las componentes. En general, cada tres valores que cumplan con el teorema
de Pitágoras son componentes de una terna pitagórica.
Vásquez y Vásquez (2016, p.62) plantean buscar ternas pitagóricas diciendo que “En esencia
lo que se busca es que al sumar dos números cuadrados se obtenga otro cuadrado. Es decir,

39 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
que la idea es tomar dos áreas que pueden juntarse y dar como resultado una tercera. El
resultado es justamente un cuadrado más grande, que se construye ubicando el cuadrado (b²),
y ubicando el espacio del otro cuadrado (a²), alrededor del primero, de forma que se construya
un nuevo cuadrado, cuyo lado será el valor de
Históricamente según Fallas (2009) “el origen de las ternas (hoy llamadas pitagóricas)
comenzó antes de Pitágoras (Siglo VI a.C.) pues hay evidencias en base al hallazgo de tablas
babilónicas que contienen algunas de estas ternas, quienes seguramente tenían algún método
para generarlas. Además, hay rastros de su uso en Egipto para generar ángulos rectos, los
cuales eran utilizados en agrimensura y construcciones”. Es decir, que el cálculo de ternas
pitagóricas representa un procedimiento matemático de muy antigua data.
Sin embargo, en criterio propio, permanecer anclado a los métodos antiguos sin repensar el
problema de las ternas pitagóricas o del teorema de Pitágoras ha sido una limitante para el
avance en la determinación eficiente y generalista de ternas.
Según Rodríguez (2014, p.6) en una terna pitagórica puede
ocurrir que puede ser primo o compuesto, es compuesto (es par) y puede
ser primo o compuesto. Ejemplos:
La forma de pensamiento expresada por el autor citado tiende a estudiar aspectos
propios de las ternas, pero no lleva a un estudio de ternas en una forma total haciendo la
consideración de todos los números naturales, lo cual le quita aspectos de generalización del
comportamiento total de las ternas.
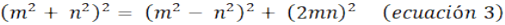
40 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Algo interesante es que Muñoz (2019) presentó la que considera la terna más grande
del mundo, pero se verá que con el teorema desarrollado en este artículo no hay limitantes
para seguir hallando ternas infinitamente. Es decir, que esta es una simple pretensión
matemática de este autor, ya que se pueden hallar millones de ternas pitagóricas más grandes
que ella al ser un valor impar, ya que la terna por el autor reseñada toma el último primo de
Mersenne descubierto en 2018.
Además, Overmars y otros (2019) plantearon su artículo “Un nuevo enfoque para
generar todas las ternas pitagóricas” donde presentan estrategias de trabajo para ternas en
base a parametrización.
Por otra parte, Vásquez y Vásquez (2016, p.61) citan a Roy & Sonia (2012), quienes proponen
una generación de ternas pitagóricas basándose en la igualdad:
Según los autores citados previamente se conocen varios resultados que se limitan a
esta condición, estableciendo que las ternas pitagóricas deben contener un número que resulte
de sumar dos cuadrados, otro que resulte de restar esos dos cuadrados y un tercero que
resulte del doble producto entre las raíces de esos números.
Sin embargo, esa relación o forma de trabajo ha sido históricamente imprecisa, ya que como
dice lo anterior varios resultados se limitan a esa condición, pero hay muchos valores de ternas
pitagóricas que no lo cumplen, por lo cual no constituye una forma de trabajo efectivo, mientras
que no se precise el cumplimiento de los cuadrados según Pitágoras.
En este sentido, se ha avanzado en por lo menos percatarse de la generación de unas
cuantas ternas partiendo del uso de 4 términos de la serie Fibonacci, pero es interesante la
generación de ternas partiendo de todos los naturales. Por poner ejemplos de lo que se quiere
decir, en el desarrollo de este artículo han surgido una serie de preguntas como las siguientes:
• ¿Hay una forma de generar ternas pitagóricas tomando cada par de números naturales
desde el 1?
41 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
• ¿Se pueden hallar ternas pitagóricas tomando en cada caso 3 números consecutivos?
• ¿Se pueden generar ternas pitagóricas tomando cada natural como el valor del cateto
menor?
• ¿A partir de la primera terna impar se pueden desarrollar métodos iterativos o
programables que generen las demás ternas con primer elemento impar o el primer
elemento par de manera que se consideren todas las ternas sin excepciones?
• ¿Se pueden diseñar fórmulas que determinen los valores de ternas con una cierta
distancia y hacer una fórmula que generalice el comportamiento de las ternas
pitagóricas?
Todas esas interrogantes y cuestionamiento son el basamento de los pensamientos que
han dado origen a este artículo que rompe con los métodos tradicionales de búsqueda de
ternas pitagóricas o de triadas que satisfagan o cumplan el teorema de Pitágoras y que serán
esbozados en forma de teoremas, formulas y métodos iterativos en el desarrollo de los
resultados del presente artículo.
1.4. Teorema de Pitágoras
Según Barrantes, Barrantes y otros (2018) “En todo triángulo que sea rectángulo (con
un ángulo de 90°), se verifica que la suma de los cuadrados de los dos catetos es igual al
cuadrado de la hipotenusa”. Esta proposición, indica el Teorema de Pitágoras, y corresponde a
la proposición 47 del libro I de los Elementos de Euclides, la cual ha tenido un valor significativo
en el avance matemático que ha sido logrado.
En efecto, en el área del álgebra y la geometría este es uno de los teoremas más famosos y
uno de los fundamentales en la historia de las matemáticas, ya que tiene cerca de 2500 años,
pero desde su descubrimiento es poco lo que se ha avanzado en la determinación efectiva de
tripletes pitagóricos
Reyes, Rondero, Acosta, Campos y Torres (2017), hablan de la relación pitagórica
42 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
(RP) y el reduccionismo pedagógico que tiene implicaciones en la conceptualización reducida
de este saber, es decir, pareciera que un número considerable de estudiantes de nivel
universitario se quedan en aspectos elementales de este conocimiento.
Reyes, Rondero, Acosta, Campos y Torres (2018, p.59) afirman que “la RP debería
conllevar a una red más amplia de conceptos y significados generados en relación al teorema
de Pitágoras, pues el mismo tiene mucha versatilidad en las matemáticas, pues se trata en la
teoría de números, el álgebra, la geometría, la trigonometría, la geometría analítica y el
cálculo”.
A criterio personal esta tendencia de pensamiento que los autores llaman reduccionismo
didáctico es asumido por muchas personas que estudian e investigan en matemáticas, quienes
se han quedado mucho con la perspectiva planteada en la tablilla Plimpton 322 y poco se han
interesado por buscar estrategias más profundas que simplifiquen desde una vez y para
siempre los procesos de búsqueda de ternas pitagóricas.
En efecto, los matemáticos en la mayoría de los trabajos de investigación se centran en
estudiar aspectos como las ternas que cumplen con una cierta diferencia entre sus dos
primeros componentes, es decir, entre a y b (los catetos) o entre sus dos últimos términos, b y
c es decir uno de los catetos y la hipotenusa, pero muy poco se han centrado en lograr
mayores avances en la generación de ternas pitagóricas, sino que en los artículos que
presentan se limitan a un estudio de posibles casos particulares.
Sobre el teorema de Pitagóras, las estudiantes Johnson y Jackson (2023) hacen una
demostración trigonométrica de dicho teorema lo cual se creía imposible. Este logro ha sido
reseñado por Sloman (2024) y también por Musso (2024) quien señala que las autoras
añadieron 10 nuevas formas de demostrar dicho teorema, aumentando el gran número de
demostraciones existentes sobre el teorema.

43 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
RESULTADOS
A continuación, se hace la presentación de los teoremas de generación de números
primos, así como de fórmulas y métodos de iteración de ternas pitagóricas que procuran ser las
respuestas a los cuestionamientos planteados en el inciso 2, 3.
2.1. Teorema 1: teoremas de ternas para n como cateto menor
Para cada número natural es posible encontrar ternas pitagóricas para los
divisores propios de igual paridad que n. Sea n el número, d un divisor propio y q el
cociente que resulta de la división exacta entonces si se cumple que:
Entonces siempre independientemente de los valores de n, d y q que cumplan con la división
exacta entonces:
En este teorema, la divisibilidad entre divisores d de igual paridad que el valor de n
cateto menor es la condición necesaria, ya que si no ocurre la divisibilidad de n entre el valor de
d no se podrá obtener la terna pitagórica que se desea encontrar. En este sentido, encontrar la
terna es la condición suficiente o la conclusión a la que se llega con la aplicación reiterativa del
teorema.
Demostración
Basta comprobar que se cumple el teorema de Pitágoras. Para ello es preciso
demostrar que la suma de los cuadrados de los dos primeros valores de la triada es igual al
cuadrado del tercer término. Es decir, debe verificarse que:
Al desarrollar el lado izquierdo de la igualdad tenemos que:

44 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Pero resulta que
Al desarrollar el lado derecho de la igualdad tenemos que:
Pero resulta que
Se puede ver que la 6.1 y la 6.2 son iguales por lo cual se verifica el teorema de
Pitágoras, en el cumplimiento de la ecuación 6.
El teorema enunciado habla claramente de que la conformación de ternas pitagóricas
solo es posible cuando se da la división exacta, pero es importante recalcar un conjunto de
aspectos que son importantes tener en consideración:
1. en el caso de que n sea primo como 3, 5, 7 entre otros primos siempre se genera una
única terna pitagórica, pero ello se debe a que 1 es el único divisor exacto del número
primo que es inferior a su tercera parte, ya que es impar.
2. Si un número compuesto tiene n divisores de igual paridad (divisores pares si el número
es par o divisores impares si el valor de n es impar) se generarán n ternas pitagóricas

45 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
con n como primer componente que corresponderá siempre al cateto menor excepto en
la terna (4,3,5)
3. En el caso del valor de n par se consideran para la generación de ternas los divisores
del número par hasta n/2 y en el caso de n impar y compuesto se consideran los
divisores hasta n/3. De esa manera se generan todas las ternas posibles partiendo del
hecho de hacer la consideración de que el valor de n sea el cateto menor
Pero el lector podría pensar que el cumplimiento de las ternas pitagóricas para valores de n
como cateto menor es insuficiente, por lo cual a continuación se especifica el cumplimiento de
las ternas para n par y n impar.
2.2. OBTENCIÓN DE TERNAS PARA PRIMER CATETO PAR
Sea n un número par cualquiera y k un número par que divida a n entonces siempre que
entonces en cada caso que se obtenga un cociente q resulta una terna pitagórica:
Si n y k son números pares tales que k divide a n (k|n) es decir:
Entonces en dicho caso siempre se cumple que:
Aclaratoria: siempre n y k deben ser pares, ya que de ocurrir que k sea impar (lo cual es
probable en divisores de números de pares, ya que admiten divisores pares e impares)
ocurriría que siempre, ya sea que se obtenga q par o impar ocurriría que qn-k sería impar, con
lo cual no sería divisible entre 2 y no sería un valor en los naturales, es decir, no cumpliría la
ecuación diofántica de ternas pitagóricas. Sin embargo, los divisores k impares generan
soluciones racionales, que satisfacen el teorema de Pitágoras, pero esa no es la idea sino
encontrar siempre soluciones enteras.
Son valores que conforman una terna pitagórica
Cada valor “n” par genera siendo primer componente tantas ternas pitagóricas como divisores
46 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
propios hasta n/2 existan.
En cada terna (a, b, c) a medida que aumentan los divisores los valores de b y de c
tienden a disminuir en relación a los divisores más pequeños. Siempre se cumple que la
distancia b-c=k.
Por ejemplo:
Tabla 1
Ternas pitagóricas a partir de 60 como cateto menor
N
k
Q
Terna (a, b, c)
60
2
30
(60, 899, 901)
60
4
15
(60, 448, 452)
60
6
10
(60, 297, 303)
60
10
6
(60, 175, 185)
60
12
5
(60, 144, 156)
60
20
3
(60, 80, 100)
60
30
2
(60, 45, 75)
Fuente: elaboración propia de los autores
Demostración:
Probamos que siempre la terna anterior es pitagórica. Tenemos que si
Lo cual se cumpliría para cada divisor entonces si sustituimos en la terna anterior puede
expresarse que:

47 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Ahora debemos probar si es cierto que:
Desarrollaremos primero el lado izquierdo de la igualdad anterior de lo cual se obtiene que:
Al desarrollar el lado derecho de la igualdad se obtiene que:
Entonces de (10.a) y (10.b) se obtiene que siempre la ecuación 10 se cumple y entonces
(forma de terna 1) cumple con generar una terna pitagórica para cada valor de que se
pueda tener siempre y cuando se dé la relación de divisibilidad.
2.3. OBTENCIÓN DE TERNAS PARA PRIMER CATETO IMPAR
Si son números impares tales que , es decir:
Entonces en dicho caso siempre se cumple que:
Son valores que conforman una terna pitagórica
Cada valor “n” impar genera siendo primer componente tantas ternas pitagóricas como
divisores propios hasta existan.

48 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
En cada terna (a, b, c) a medida que aumentan los divisores los valores de b y de c
tienen a disminuir en relación a los divisores más pequeños. Siempre se cumple que la
distancia
15 tiene 3 divisores propios pares hasta que son 1, 3, 5,
Tabla 2
Ternas pitagóricas a partir de 15 como cateto menor
n
K
2q+1
q
q(n + k)
q(n + k)+k
Terna (a, b, c)
15
1
15
7
7(15+1) =112
7(15+1) +1=113
(15,112,113)
15
3
5
2
2(15+3) =36
2(15+3) +3=39
(15, 36, 39)
15
5
3
1
1(15+5) =20
1(15+5) +5=25
(15,20,25)
Fuente: elaboración propia de los autores.
Demostración:
Probamos que siempre la terna anterior es pitagórica. Tenemos que si
Lo cual se cumpliría para cada divisor entonces si sustituimos en la terna anterior puede
expresarse que
O bien
Ahora debemos probar si es cierto que:
Desarrollaremos primero el lado izquierdo de la igualdad anterior de lo cual se obtiene que:
q

49 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Ordenando en forma decreciente respecto a términos con q podemos escribir
Aplicando agrupación de términos y sacando factor común resulta que:
Al desarrollar el lado derecho de la igualdad se obtiene que:
De lo antes expresado tomando como factor común queda:
Entonces de (14.a) y (14.b) se obtiene que siempre se cumple la (ecuación 14) y entonces la
(forma de terna 2) cumple con generar una terna pitagórica para cada valor de n, k y q que se
pueda tener siempre y cuando se dé la relación de divisibilidad entre n y k ambos impares.
2.4. Forma alternativa del teorema 1.
Si se parte de (ecuación 4) entonces al despejar y sustituir en la (ecuación 5)
queda la forma de terna
Como puede verse la forma de la terna resultante en (ecuación 15) es archiconocida,
pero no se pueden tomar valores arbitrarios como históricamente se ha hecho, por una especie
de tanteo o prueba de ensayo y error, sino que los valores de siempre están conectados
siendo siempre y siendo un divisor propio de , por lo cual es pertinente partiendo de d
buscar no cualquier divisor sino aquellos que tengan la misma paridad de de manera que se
asegure que siempre el valor del numerador es par y en consecuencia siempre de valores
enteros al ser divisible entre 2, para que ciertamente en todo caso se pueda hallar la terna.

50 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Sin embargo, la terna en la forma de la (ecuación 4) es más fácil de plantear, pues no requiere
ni potencias cuadradas ni complejas operaciones de división, lo cual tiende a complicar mucho
más los cálculos de las ternas cuando los números crecen excesivamente. Esto
contribuirá a poder desarrollar una forma de programar ternas pitagóricas basadas en la
divisibilidad del valor de n usado sea este par o impar.
2.5. Ternas pitagóricas con todos los naturales
Según Fallas (2009) y Arenzana (2019) es famoso y conocido el uso de la sucesión de
Fibonacci para generar algunas ternas pitagóricas. Eso me llevó a pensar en el hecho de
generar ternas pitagóricas que se formaran a partir de todos los números naturales y que fuese
mucho más completo que las ternas generadas con Fibonacci.
2.5.1. Ternas pitagóricas con un par de números consecutivos
Con los números naturales sin excepciones tomando cada par de ellos, es decir, 1 y 2, 2
y 3, 3 y 4 y así sucesivamente es posible generar todas las ternas con primer componente
impar y donde la distancia c-b=1 por medio de la terna de la forma:
Es decir, que se cumple para todo valor consecutivo que:
Demostremos que la ecuación anterior se cumple para todo par . En
efecto, basta comprobar que el lado izquierdo da el mismo resultado que el lado derecho al
sustituir.
Entonces al desarrollar el lado izquierdo de (ecuación 16) nos queda:

51 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Al desarrollar el lado derecho de (ecuación 16) nos queda:
De (16.a) y su igualdad con es evidente que la se cumple para todo par
de la forma la forma de terna 3
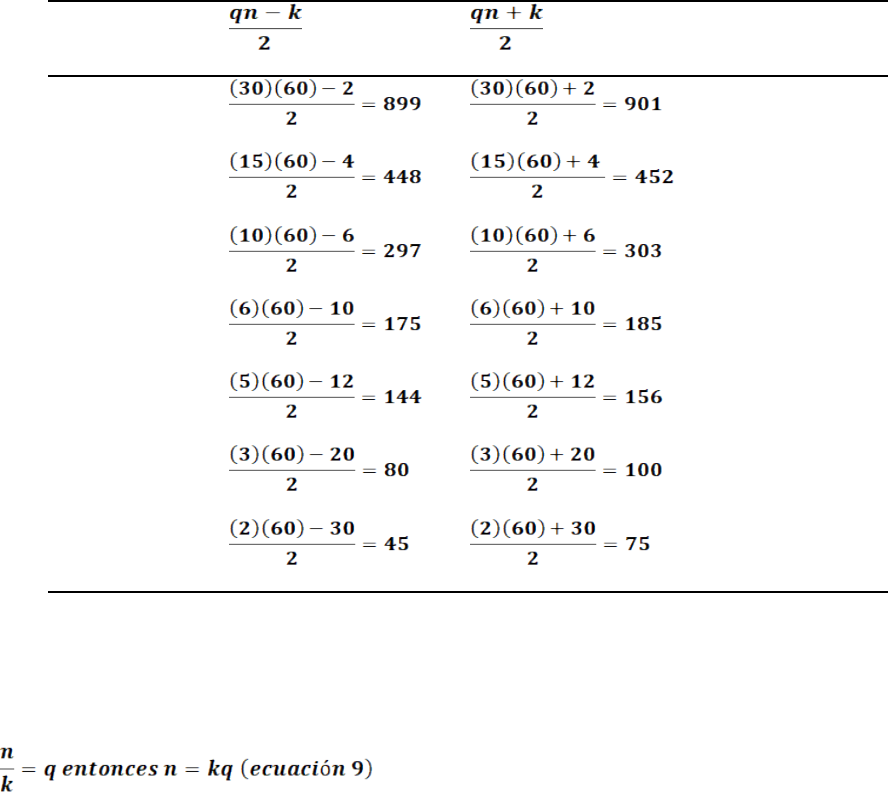
2.5.2. Ternas pitagóricas con un trío de números consecutivos
Para valores de consecutivos desde 1 y hasta infinito es posible formar ternas de la
forma:
Es decir, que se cumple para todo valor a, b y c consecutivos que:
Demostremos que se cumple para toda triada. En efecto, basta comprobar que el lado
izquierdo de la igualdad da el mismo resultado que el lado derecho al sustituir
Entonces al desarrollar el lado izquierdo de nos queda:
Al desarrollar el lado derecho de nos queda:
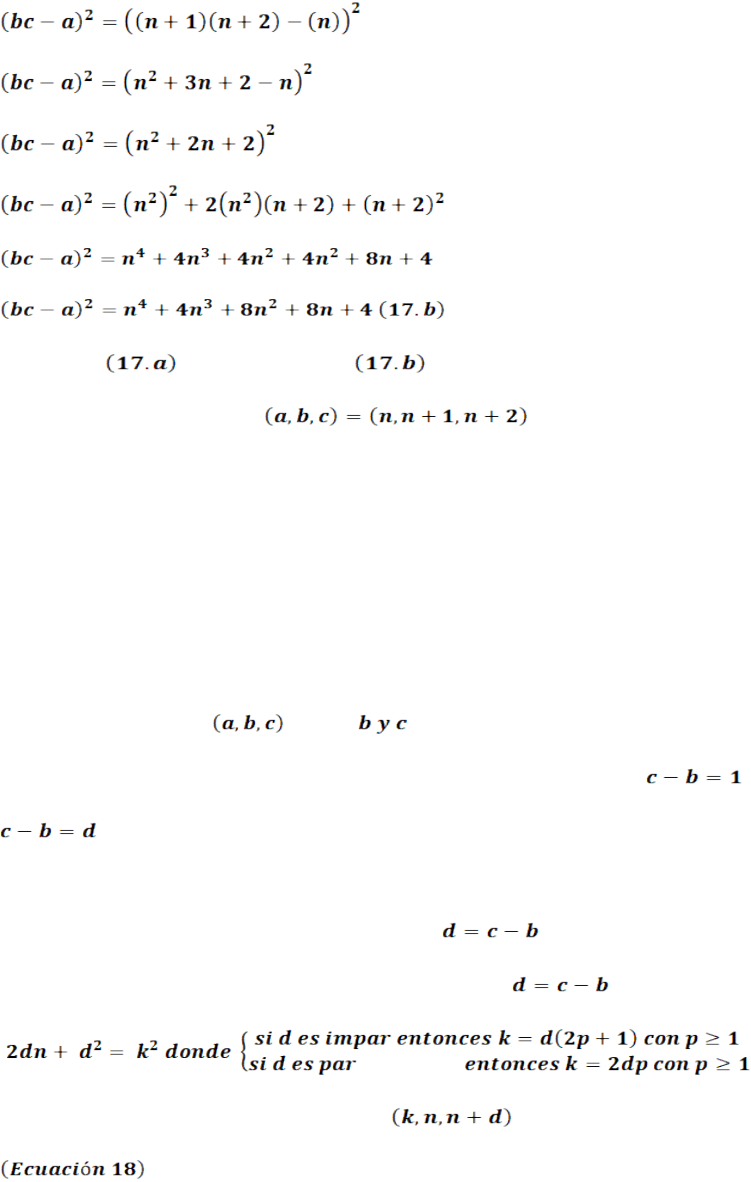
52 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
De y su igualdad con es evidente que la (ecuación 17) se cumple para
toda triada par de la forma y se verifica la forma de terna 4
En estos incisos el lector puede ver la posibilidad de generar ternas con primer
componente impar con un par de valores consecutivos y de generar ternas con el primer
componente par con un trío de valores consecutivos.
2.6. Fórmula generadora de ternas de distinta distancia entre b y c
Una de las cosas que es frecuentemente estudiada por los matemáticos es la
generación de ternas donde tienen un determinado valor y en este artículo se
expondrá un teorema que permite generar todas las ternas desde hasta cierto
.
2.6.1 Teorema 2:
Generación de ternas con cierta distancia
Para generar las ternas con una cierta distancia se aplica la expresión:
Y la terna resultante en cada caso es

53 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
2.6.2 Aplicabilidad del teorema 2
En este teorema se cambia el valor de d con el cual se quieran hallar ternas y se evalúa
el valor de k inicial según la rama correspondiente para determinar el valor de n que cumple la
primera ecuación, para cada terna siguiente se vuelve a incrementar k y se busca de nuevo el
valor de n y así sucesivamente generando en cada caso la terna de la forma
correspondiente.
Si se comienza en k=1 se pueden generar 100 o más ternas con distancia d=1 y
siguiendo el teorema se pueden generar 100 ternas para cada distancia desde d=1 hasta
d=100. Sin embargo, el teorema sigue funcionando para cualquier distancia d que se desee
hallar ternas pitagóricas.
Demostración: es fácil ver a partir de que al aplicar el teorema de Pitágoras se
cumple que
Y de lo anterior se mira el cumplimiento de la expresión en el teorema
Que se obtiene de simplificar los términos , hacer su cancelación en ambos miembros de la
igualdad y girar la expresión resultante. Para ejemplificar el teorema anterior buscaremos las
ternas para distancias donde da números pares.
Tabla 3
Ternas pitagóricas cuyas distancias b-c = 4f con f = 1, 2, 3, 4
Ternas de
distancia C-B=4
Ternas de
distancia C-B=8
Ternas de distancia
C-B=12
Ternas de
distancia C-B=16
(8,6,10)
(16, 12, 20)
(24,18,30)
(32, 24, 40)
(12,16,20)
(24, 32, 40)
(36,48,60)
(48, 64, 80)

54 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
(16,30,34)
(32,60,68)
(48,90,102)
(64,120,132)
(20,48,52)
(40,96,104)
(60,144,156)
(80,192,208)
(24,70,74)
(48,140,148)
(72,210,222)
(96,280,296)
(28, 96,100)
(56,192,200)
(84,288,300)
(112,384,400)
Fuente: elaboración propia de los autores
Tabla 4
Ternas pitagóricas cuyas distancias b-c = 4f-2 con f = 1, 2, 3, 4
Ternas de
distancia C-B=2
Ternas de
distancia C-B=6
Ternas de distancia
C-B=10
Ternas de
distancia C-B=14
(4,3,5)
(12, 9, 15)
(20,15, 25)
(28, 21,35)
(6,8,10)
(18, 24,30)
(30,40,50)
(42, 56, 70)
(8,15,17)
(24,45,51)
(40,75,85)
(56,105,119)
(10,24,26)
(30,72,78)
(50,120,130)
(70,168,182)
(12,35,37)
(36,105,111)
(60,175,185)
(84,245,259)
(14, 48,50)
(42,144,150)
(70,240,250)
(98,336,350)
Fuente: elaboración propia de los autores
Para hallar algunas de las ternas con distancias impares el lector puede desarrollar
cálculos para ejercitar la funcionabilidad del teorema en la búsqueda de ternas pitagóricas.
Como es visible el teorema 1 y el teorema 2 brindan características de iteratividad y fácil
evaluación de ternas que pueden ser fácilmente programables en lenguaje C u otro lenguaje de
programación

55 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
DISCUSIÓN
2.7. Ternas pitagóricas que escapan del primer teorema.
Históricamente el misterio de las ternas pitagóricas es fascinante y atrayente al punto
que ha traído de cabeza a muchos matemáticos y aún 2500 años después de su
descubrimiento es un interesante tema de estudio.
De desarrollar el teorema 1 que se basa en divisibilidad y comparar con ternas
pitagóricas online se pudo avanzar en el conocimiento que se tiene acerca de las ternas
pitagóricas y las posibilidades de formación tomando el valor de en la terna y
llevando a cabo observaciones acerca de la separación entre y los posibles divisores del
valor inicial de la terna que siempre debe ser el cateto menor. Entonces al revisar información
diversa se pudo observar que el tema de las ternas pitagóricas va mucho más allá del simple
análisis y trasciende muchas formas de pensamiento
Lo dicho puede ser evidenciado al revisar tablas y hacer una detallada observación de
las mismas, lo que conlleva a realizar nuevas consideraciones importantes a la hora de querer
hallar todas las ternas para un cierto cateto menor
A continuación, se presenta una tabla y se hace un análisis respectivo de los valores
contenidos en las ternas
Tabla 5
Algunas ternas pitagóricas primitivas
Fuente: https://es.wikipedia.org/wiki/Terna_pitagórica
( 3 , 4 , 5 )
( 5, 12, 13)
(8, 15, 17)
( 7, 24, 25)
( 9, 40, 41)
(11, 60, 61)
(12, 35, 37)
(13, 84, 85)
(16, 63, 65)
(20, 21, 29)
(28, 45, 53)
(33, 56, 65)
(36, 77, 85)
(39, 80, 89)
(48, 55, 73)
(65, 72, 97)

56 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
El lector puede apreciar que en las dos primeras filas aparecen números cuya diferencia
entre los valores son de 1 y de 2 al comparar sus valores. Sin embargo, resulta
sumamente interesante analizar las líneas 3 y 4 de la tabla anterior, ya que los primeros
números entre ellos 20, 28, 33, 36, 39, 48 y 65 no son ningunos de ellos divisibles entre las
distancias de b y c de cada triada, es decir que:
• 20, 28 y 36 no es divisible 8,
• 33 y 39 no son divisibles entre 9,
• 48 no es divisible entre 18 y
• 65 no lo es entre 25.
Lo anterior es muy significativo, pues permite optimizar el teorema 1, pues las
diferencias que hay entre los valores b y c de las ternas se relacionan con la multiplicidad de
los divisores (sean pares o impares) o cuadrados de los mismos divisores siempre y
cuando los nuevos productos, aunque no sean divisores directos del cateto menor sean
valores menores n/2 si n es par o menor que n/3 si n es impar y productos de igual
paridad que n, siendo siempre n el cateto menor
Tabla 6
Lista de ternas Pitagóricas (triadas pitagóricas)
A
B
C
A
C
B
A
B
C
3
4
5
44
117
125
120
209
241
5
12
13
44
483
485
132
475
493
7
24
25
48
55
73
133
156
205
8
15
17
51
140
149
135
352
377
9
40
41
52
165
173
136
273
305
11
60
61
57
176
185
140
171
221
12
35
37
60
91
109
145
408
433

57 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
13
84
85
60
221
229
152
345
377
15
112
113
65
72
97
155
468
493
17
144
145
68
285
293
160
231
281
19
180
181
69
260
269
161
240
289
20
21
29
75
308
317
168
425
457
21
220
221
76
357
365
175
288
337
23
264
265
84
187
206
180
299
349
24
143
145
84
437
445
189
340
389
25
312
313
85
132
157
203
396
445
27
364
365
87
416
425
204
253
325
28
45
53
88
105
137
207
224
305
29
420
421
93
476
485
225
272
353
31
480
481
95
168
193
228
325
397
32
255
257
96
247
265
252
275
373
33
56
65
104
153
185
261
380
461
36
77
85
105
208
233
280
351
449
39
80
89
115
252
277
297
304
425
40
399
401
119
120
169
319
360
481
Fuente: https://www.vaxasoftware.com/doc_edu/mat/3pitafac.pdf
Además, en la tabla 6 puede apreciarse más claramente lo dicho para tabla 5 de la
existencia de distancias que no son exactamente divisores del cateto menor n, sino una
potencia de uno de ellos o un producto de dos o más de ellos siempre y cuando dicho producto,
aunque no sea divisor exacto cumpla con tener la misma paridad del cateto menor.
58 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
CONCLUSIONES
Los dos teoremas presentados en este artículo son de gran importancia porque si bien el
primero permite apreciar la dependencia de las ternas pitagóricas de la divisibilidad del cateto
inicial y tener un criterio para generar ternas pitagóricas, el segundo permite encontrar ternas
tomando en cuenta el aspecto de la distancia existente entre el segundo y tercer componente
de cada triada, aspectos que permitirán generar las ternas con más eficiencia y sin la tendencia
a la improvisación, el ensayo y error, entre otros aspectos característicos de métodos previos.
Por otra parte, los teoremas tienen una cualidad de generalización importante, pues
permite el primero buscar todas las ternas para cada uno de los números naturales mayores
que 2 al tomarlo como cateto inicial lo cual permite la generación ordenada de las ternas si se
programa en cualquier lenguaje de cómputo como C, Pascal, XXXX , mientras que el segundo
permite tomar una determinada distancia entre los dos componentes y generar cualquier
cantidad de ternas pitagóricas donde los componentes tienen una cierta diferencia.
En cuanto a las ternas indicadas con las ecuaciones 4 y 18 que funcionan para un par o
una triada de números naturales consecutivos se puede ver su utilidad para generar todas las
ternas de distancia 1 o 2 respectivamente entre los dos últimos componentes de cada terna
que surgen de su evaluación.
Además, es importantísima la última observación que es planteada en el inciso 3.7., ya
que dicha forma de trabajo con potencias de un mismo divisor o productos de sus divisores (de
igual o diferente paridad) del cateto menor que generen productos de igual paridad de n son
generadores también de ternas pitagóricas, lo cual complementa excelentemente el trabajo con
el primer teorema.

59 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
REFERENCIAS
Alegría, P. (2018). La solución matemática más larga de la historia. Recuperado de
https://www.abc.es/ciencia/abci-solucion-matematica-mas-larga-historia-
201804022054_noticia.html
Arenzana, V. (2019). Ternas pitagóricas. Recuperado de https://vicmat.com/ternas-pitagoricas/
Artacho, A. (2022). 2023 y las ternas pitagóricas. Recuperado de
https://matematicascercanas.com/2022/12/28/2023-y-las-ternas-pitagoricas/
Barrantes López, M., Barrantes Masot, M., Zamora Rodríguez, J., & Mejía López, Á. (2018). El
Teorema de Pitágoras, un problema abierto. Revista Matemática de Educación
Matemática Unión, 54, 92–112. Recuperado de http://www.fisem.org/web/union y
http://www.revistaunion.org/
Fallas, J. J. (2009). Ternas pitagóricas: métodos para generarlas y algunas curiosidades.
Revista Digital: Matemática, Educación e Internet, 9(2), 1–21. Cartago, Costa Rica:
Instituto Tecnológico de Costa Rica.
González, P. (2008). El teorema llamado de Pitágoras: Una historia geométrica de 4000 años.
Sigma, (32).
Graña, M., Jerónimo, G., & Ariel, P. (2009). Los números: De los naturales a los complejos (1.ª
ed.). Buenos Aires, Argentina: Ministerio de Educación de la Nación, Instituto Nacional
de Educación Tecnológica. ISBN: 978-950-00-0748-1.
Jiménez, D. (2013). Aritmética (3.ª versión). Valparaíso, Chile: Universidad de Valparaíso.
Jiménez, R., Gordillo, E., & Rubiano, G. (2004). Teoría de números para principiantes (2.ª ed.).
Bogotá, Colombia: Universidad Nacional de Colombia. ISBN: 958-701-372-7.
Johnson, C., & Jackson, N. (2023). An impossible proof of Pythagoras. AMS. Recuperado el 18
de marzo de 2023 de https://meetings.ams.org/
Lane, S. M., & Birkhoff, G. (1999). Algebra (Vol. 330). American Mathematical Society: Chelsea
Publishing Company.

60 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Mansfield, D. & Wildberger, N. J. (2017). Plimpton 322 is Babylonian exact sexagesimal
trigonometry. Historia Mathematica. Recuperado de
http://www.sciencedirect.com/science/article/pii/S0315086017300691
Martín, A. (2023). El teorema de Pitágoras está en una tabla babilónica 1.000 años anterior al
nacimiento de Pitágoras.
Muñoz, R. (2019). La terna pitagórica entera más grande de la actualidad. Recuperado de
https://www.academia.edu/38777167/
Musso, M. (2024). Estas dos estudiantes revelaron diez nuevas formas de explicar el teorema
de Pitágoras. Recuperado de https://es.wired.com/articulos/estas-dos-estudiantes-
revelaron-diez-nuevas-formas-de-explicar-el-teorema-de-pitagoras
Overmars, A., Ntogramatzidis, L., & Venkatraman, S. (2019). Un nuevo enfoque para generar
todas las ternas pitagóricas. Recuperado de
https://www.researchgate.net/publication/331777611
Pérez Porto, J., & Merino, M. (2009). Definición de números naturales. Recuperado de
https://definicion.de/números-naturales/
Pina-Romero, S. (2022). Los números naturales. Recuperado de
https://www.todamateria.com/numeros-naturales/
Ramos, F. (2010). Aritmética: Teoría y práctica. (1.ª ed.). Lima, Perú: Empresa Editora Macro.
ISBN: 978-612-4034.
Reyes, A., Rondero, C., Acosta, J., Campos, M., & Torres, A. (2017). Reduccionismo didáctico
y creencias de profesores acerca del teorema de Pitágoras. Bolema: Boletim de
Educação Matemática, 31(59), 968–983.
Reyes, A., Rondero, C., Acosta, J., Campos, M., & Torres, A. (2018). Un acercamiento a la
relación pitagórica a través del cálculo de ternas. European Scientific Journal, 14(6).
ISSN: 1857-7881.

61 Revista Multidisciplinar Epistemología de las Ciencias | vol. 1, núm. 1, 2024
Robson, E. (2002). Words and pictures: New light on Plimpton 322. The American Mathematical
Monthly, 109(2), 105–120. https://doi.org/10.1080/00029890.2002.11919845
Rodríguez-Roselló, M. (2014). La naturaleza trans-pitagórica de los números primos.
Recuperado de https://vixra.org/pdf/1407.0014v2.pdf
Roldán, A. (2024). Teoría de la divisibilidad. Recuperado de
https://www.academia.edu/13840762/
Roy, T., & Sonia, F. (2012). A direct method to generate Pythagorean triples and its
generalization to Pythagorean quadruples and n-tuples. Recuperado de
https://www.semanticscholar.org/
Sloman, L. (2024). 2 high school students prove Pythagorean theorem. Here’s what that means.
Scientific American. Recuperado el 7 de junio de 2024.
Vásquez, M., & Vásquez, M. (2016). Generando números de Pitágoras. Recuperado de edison-
timbe-maskana-7106.pdf
Villatoro, F. (2017). El significado matemático de la tablilla babilónica Plimpton 322. La Ciencia
de la Mula Francis. Recuperado de https://francis.naukas.com/2017/09/07/el-significado-
matematico-de-la-tablilla-babilonica-plimpton-322/
Villarroel, A., & Villarroel, F. (2023). Del test de Chika a un criterio general de divisibilidad entre
cualquier número primo o compuesto: Características y consecuencias. Revista Digital
Matemática, Educación e Internet, 23(2). Recuperado de https://tecdigital.tec.ac.cr/
Zaldívar, F. (2012). Introducción a la teoría de números. México: FCE. ISBN: 978-607-16-0738-
61.